WAR CASUALTIES
By
Albert G. Love,
SECTION II
[Note: Section II is intended for use by only such
as are interested in the technical details in the development of the material
in Section I.]
IV. EXPLANATORY NOTES AND
DEVELOPMENT OF FORMULAE.
Q. EXPLANATORY NOTES.
The basic data and material used in this study are from the sources stated
in the reference list. Much of the material is from the unpublished statistical
tables and sheets on file in the office of the Surgeon General, which are
referred to in the list. New tabulations were made from the statistical
cards to show how many cases left sick report during the first seven days,
the second seven, etc., during the World War, as follows:
1. All cases wounded by gunshot missiles, and all deaths and disability
discharges resulting therefrom.
2. All cases wounded by poisonous gases, and all deaths and disability
discharges resulting therefrom.
3. (a) A sample of approximately 150,000 out of about 450,000 disease
and nonbattle injury cases in the American Expeditionary Forces during
the last six months of 1918. The sample included the same proportion of
each diagnosis.
(b) All of the deaths from diseases and nonbattle injuries in the American
Expeditionary Forces during 1918.
4. All deaths and discharges for disability among troops in the United
States during 1918.
The task of tabulating a sufficiently large sample of the duty cases
in the United States during 1918 was too great a one to be undertaken with
the time and personnel available. Similar data were available, however,
for the troops in the United States during 1925-1927, and it was assumed
that there was no material difference in the duration of treatment of such
cases and of similar ones during 1918. Consequently those data available
for the 1925-1927 cases were used as 1918 experience with the necessary
slight modifications as indicated in Figs. 80 and 82.
In the absence of more exact information, estimates were used in some
instances, as noted in the appropriate places. Whenever this was done all
available data were checked to test the estimated results.
The sources of information, the method of arriving at such estimates
as were used, and the changes which were made in the basic data are noted
in connection with the various Figures.
R. DEVELOPMENT OF FORMULAE
53. Patients leaving sick report. --- The data
for Figs. 21-64 are largely from formulae. Figs. 79-98 inclusive, show the
method of developing them. The basic material as tabulated, shows how many
patients of the duty, death, or disability groups left sick report during
the first, second, third week, etc. The numbers leaving sick report each
week were divided by the total in thousands to reduce each weeks cases to
proportional parts per 1000 of the total number.
54. Graduation of material. --- In some instances
attempts were made to fit this basic material to second or third order parabolas
and also to Pearsonian curves, but the results were not satisfactory. It
soon became apparent that there was a very definite geometrical progression
relationship between the groups of cases leaving sick report by time intervals
or remaining on it, and that all of the curves were exponential in character.
Inspection showed that this type of curve fitted the observed points quite
well with only a few exceptions. The apparent failure to fit was due usually
to imperfections in, or incompleteness of, the basic material; but in some
instances, the necessity of relating the graduated data to those from other
curves resulted in the use of a poorer fit than could have been obtained
otherwise.
The exponential curve not only best fitted the observed points, but it
graduated also satisfactorily the grouped experience beyond the 14th or
20th week; i.e., the limits of the tabulations by weeks.
55. Patients remaining on sick report. --- During
the early stages of this work, the data for leaving hospital, or sick report,
were first smoothed by fitting them to an exponential curve; but after a
short time it was found that as satisfactory results could be obtained by
omitting that step and passing directly from the ungraduated Leaving
to the ungraduated Remaining.
To find the number of patients from an original 1000 remaining sick at
the end of the first week, either the graduated, or ungraduated, number
leaving was deducted from 1000. From the remainder so obtained, the number
leaving during the second week was subtracted to find the number remaining
at the end of that time. This process was continued through the 14th, and
in some instances through the 20th week. As stated, the number remaining
beyond that time was ultimately distributed by the formulae obtained.
The following table shows the general methods of handling the material
and the results obtained in this instance.
Table 29.---Number
of patients among white enlisted men in the United States, 1925-1927, inclusive,
leaving sick report during each week; and also the number remaining on
sick report at end of each week.
56. Exponential curve. ---
a. One section curve. --- The basic formula of the exponential
curve used was

In graduating the Leaving material, Y1 designates the number
of patients leaving during each week (x7) ; and likewise in
graduating the Remaining data, Yr equals the number of patients
remaining at the end of each week (x7) --- Where x represents
a period of one week, or seven days, it is written x7; and where
it represents a five day period, x5.
The basic ungraduated data were first plotted on arithmetic-logarithmic
paper, as is shown by Fig. 79. In some instances where the material was
homogenous, as with cases wounded by poisonous gases or by gunshot missiles
(See Figs. 87 and 88),
a one section curve was sufficient.
b. Two section curve. --- In another class of cases, such as
hospital cases of disease and nonbattle injury patients, certain ones like
compound fractures of the femur and pulmonary tuberculosis which required
prolonged treatment, were not in the proper proportion to those needing
only a few days in hospital to permit of a fit by a one section curve.
In such instances there were relatively more short than long duration cases,
and a two section curve was required with the general formula
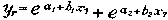
The sub 1 and sub 2 appended to the a and b designate the first (1)
and second (2) section of the curve (See Fig.
82).
c. Three section curve. --- In a third class of cases; such as
those of patients treated in hospital and quarters in the United States
in 1925-1927, the short duration treatment ones, such as the majority of
those in quarters, were relatively so much more numerous than the medium
and long duration cases, that a three section curve was required with the
general formula (See Fig. 80)
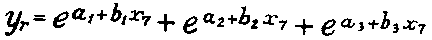
d. Plus and minus section curve. --- In a few instances where
there was too large a proportion of long duration cases for the short duration
ones, it was found necessary to use a two section curve with the second,
a minus one.
Here the formula was

e. Method of fitting. In fitting the two or three section curves,
the second or third section, as the case might be, with the long duration
cases and the proper proportion of medium and short duration ones, was
fitted first. For this purpose, the observed data were plotted on arithlog
paper, and a straight line was drawn through the lower end of the material.
The angle of this line was determined by its fit of the observed points
in that section, and also by the apparent accuracy of the graduation of
the grouped material beyond the end of the available tabulation. This latter
point was tested by comparing the total of the graduated and ungraduated
material beyond the end of the available tabulation; and also by a careful
check against the detail of the basic data, which although scattered and
irregular, showed quite definitely the general trend and time limits of
treatment.
The material so graduated was next subtracted from the ungraduated total.
The remainder was then plotted on the same sheet of arithmetic log paper,
and the second or first sections fitted. In every instance, a number of
trials was necessary before a satisfactory fit was obtained.
The sum of the different sections as graduated was summated by additions
or subtractions, as required, and the graduated total compared with the
ungraduated one.
In order to hold the higher points fixed, the fitting was by selected
points rather than by the least square method. The points used for fitting
were usually two observed ones for each section; but in some instances
where the graph or trial showed that it was necessary, the points used
were selected rather than observed.
f. Normal equation. --- The normal equation used was log to base
e of b of the equation
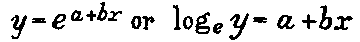
The value of each x chosen with the loge of its corresponding
y was substituted in two equations, which were then solved for a and
b. This gave a formula of the general form
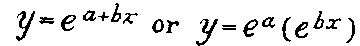
Here ea represents the original height of the curve; and
eb the numerical value of the ratio between the height at any
time (x) and that of the next following it, or in other words, the slope
of the curve. The y then is a function of x, and varies as x varies.
g. Illustration of use of formula. --- In illustrating the method
of developing the specific formulae, in the interest of simplicity the
formula of a one section curve will be used. Thus the formula in Fig. 87, showing the number of gas cases remaining
in hospital at the end of each week, is
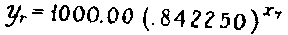
The 1000.00 is the ea; and the .842250, the eb.
The curve then starts with 1000.00 patients of whom .842250 X 1000, or
842.25, are remaining in hospital at the end of one week (x7)
; and then of this remaining group (842.25) the same fraction .(.842250)
or 842.25 X .842250=709.39 are remaining at the end of the two weeks, etc.
h. Change in size of basic group and time interval.---To convert
the formula into terms of 1 patient, simply. divide by 1000 and then

The ebx7 is in terms of seven day periods. To convert it
into terms of one day (ebx1) take the seventh root of it; and
then to change the result into terms of any other period, as, for example,
a five day one (ebx5) as used here, raise it to the fifth power.
Thus from the above.
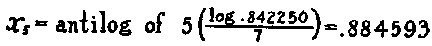
Then the formula by 5-day periods is
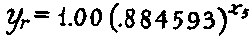
Yr then is the number of patients remaining in hospital at
the end of successive five day periods. If, however, it is necessary to
find directly the fraction of a patient remaining at the end of any
other period, as for example one year (365 days), multiply as above by
that number instead of by 5.

If the ea is 1.00, on the 365th day, .000130 of 1 patient
will still be in hospital; but if the ea is 1000.00, there will
be .13 (See Fig. 87).
To convert the ea into 100.00 patients, so that those remaining
at any time will be in terms of percentages, divide the formula showing
1000.00 by 10. Then the formula will be
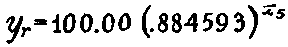
2 Percentage of patients who have left hospital. --- To find
the percentage of patients who have left the hospital, subtract the number
remaining in hospital from the original 100.00.

Expressed in general terms, the formula is
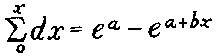
i. Graduated increase in the number of patients on sick report or
in hospital. --- Cases of sickness and injury occur from day to day.
Patients who are admitted to sick report remain under treatment for varying
periods of time, depending chiefly upon the severity of illness or injury,
but to a certain extent upon the proximity of the hospital to the troop
areas, the facility for returning the men to the organization, etc. Of
those admitted to sick report, some will have returned to duty by the end
of the first period (5 days in this case), others will go out during the
second one, while some will remain a longer time, and a few even a year
or more. During the second period, in addition to the cases coming in,
a certain number of patients will be remaining from those admitted during
the first one. Also during the third period, in addition to those admitted,
cases will be remaining from the first and second ones. And so, the increase
in the number of patients will continue as time advances, until all of
the first group of cases admitted have left sick report, which, for all
practical purposes, will be at the end of one year. After that time the
number of patients leaving sick report during each period by return to
duty, deaths, or discharges for disability, will equal the number admitted.
j. Integration of basic formula. ---To find then the number of
patients on sick report, or in hospital as the case may be, at any time,
add to the number admitted during the period, the number remaining from
all preceding ones. For this purpose the basic formula is integrated between
the beginning (M day) and the constantly advancing time, x5.
Using the basic formula with one section, the integrated formula is
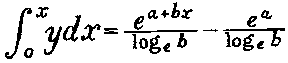
Substituting the values already found, and using one seventh of the
loge b, the formula for gas patients shows the number of gas
patients in hospital at the end of each 5 day periods
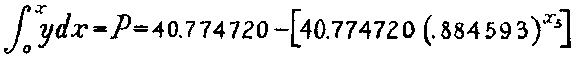
To find the total patients in hospital on any day, the day's basic admissions
must be added to the P found from this or any similar formula.
The patients (P) include all who will ultimately return to duty, die,
or be discharged as physically disabled. The number who are disposed of
in other ways is so small that it can be omitted from consideration.
k. Formulae for deaths and disability discharges, which have occurred.---
The total number of patients who have left hospital at any time by
death, disability, discharge, or duty equals those who have been admitted
less the number sick in hospital. This is also true of death and disability
cases when considered separately. The integration of the basic formula
shows how many cases, which, will ultimately result in death or discharge,
are in hospital. Then the difference between that group in hospital and
the total deaths or disabilities expected among the cases which have been
admitted, constitute the number of fatalities or disability discharges
which have already occurred.
All of the special formulae relating to death or disability cases are
expressed here as parts of the total cases [See Fig.
97, (1) and (2) ]. Thus, for every patient wounded by gas who is admitted
to hospital, .017306 will die; and if there are 5 cases admitted there
will be 5 times .017306, or .086532, fatalities. The basic formula for
the eventually fatal gas cases remaining in hospital from 1000.00 of them
admitted on any day is (Fig. 97)
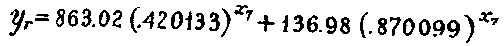
Changing each ebx7 to ebx5; reducing the sum of
the two ea from 1000.00 to 1.00 by dividing each by 1000.00;
multiplying each resulting ea by .017306 to reduce the deaths
to parts per total cases; and then integrating
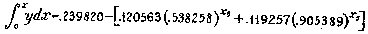
This formula shows the gas cases in hospital, who will eventually die.
At the end of 30 days the number of such cases is
. 239820 -- (.002932 + .065689) = .171199
As above, the total patients who have died or who will die out of 5
gas cases, is .086532. Consequently the formula for those who have died
is
.086532x5 -- the above formula
At the end of 30 days, or after 6 five day periods, it will be
6 (.086532) --.171199 = .347993
Then at the end of 30 days, if 30 gas cases have been admitted at the
rate of 1.00 per day, .35 have died, and .17 patients, who are in hospital,
will die.
.35 + .17 = .017306 X 30 = .519180
l. Multiple section curves. --- When two or three section exponential
curves are used, the method of developing the formulae from them is the
same as that used for a one section curve; and the only additional step
which is required is the summation of the different sections.
S. COMPUTATION OF DATA FOR
SHORT DURATION CASES.
57. Percentage leaving hospital each day by return
to duty or death. --- Calculate from the formulae on Figs. 90, 91, and
92 for duty cases; and from the last ones on Figs. 96, 97, and 98 for death
cases, the percentage of each group who return to duty or die on each day
up to and including the tenth. These data are shown by Tables 26 and 30,
respectively.
The figures are cumulated and show the percentage of duty or death cases
which occur during any period from the beginning of the first day the end
of the tenth
The percentage leaving hospital on any one day by duty, death, etc.,
can be found easily by subtraction.
Table 30.---Percentage
of the total deaths in hospital which occurred during the first ten days
from the three classes of cases in the American Expeditionary Forces.
58.---Average days of treatment. - As an illustration
of the method, let us find the average duration of treatment for gassed
cases who die in ten days or less.
a. Divide the percentage of death cases leaving hospital (dying) during
each day from the first day to the tenth, by the total leaving (dying) during
the ten days. The results expressed in parts per 100 show the percentage
of those dying in ten days or less who died on each day from the first to
the tenth. (see column 4, Table 31).
b. Beginning with 100; that is, the total percentage to die in 10 days,
subtract successively the number leaving hospital (dying) during each day
from the first to the tenth The results show the percentage of the 10 day
fatal cases remaining in hospital each day (see column 5, Table 31).
c. Reduce the results to the basis of one case instead of 100 % (see
column 6, Table 31) and summate. The total shows the eventual death cases
in hospital at the end of ten days from the group remaining under treatment
from one to ten days, when the daily admission rate of gassed cases who
die during period is 1.00.
Table 31.---Method
of finding the eventually fatal gassed cases in hospital at the
end of ten days among those that die in ten days or less, when the daily
admission rate from the group is 1.00.
With an admission rate of 1.00, the eventual death cases under treatment
(4.55) is the same as the average days treatment for each one. Table 32
shows the average duration of treatment of duty and death cases admitted
as sick, gassed, and gunshot wounded, and whose maximal days of treatment
are from one to ten. Thus of the fatal gassed cases which survive
five days or less, the average days was 2.77; and for the group surviving
ten days or less, it was 4.55.
In Table 32, the data for "Duty cases" are computed from those
for "Duty cases" in Table 26 in same way as Col. 6, Table 32 '(gassed)
are from those in Table 31. The data for "Death cases" in Table
32, are calculated similarly from those in Table 30.
Table 32.---Average
duration of treatment of cases in hospital who will return to duty or die
at any time between one day or less, and ten days or less.
59. Patients in hospital on the maximal day.
As stated above, among gassed cases who eventually die and for whom
the duration of treatment is from one to ten days, there are 4.55 cases
in hospital on the tenth day, when the daily admission rate from such cases
is 1.00 per day.
a. In the first place however, only 63.77% of the fatal gassed cases
die within ten days. Consequently to convert the data into terms of total
gassed cases which are fatal, multiply the 4.55 by 63.77%. The results
show that when the daily admission rate for fatal gassed cases of
all durations is 1.00, that among the cases surviving from one to ten days,
there are 2.90 (4.55 x 63.77%) such patients in hospital on the tenth day.
b. In the second place, only 1.73 % of all gassed cases treated
in hospital are fatal. Consequently to translate the data to the basis
of 1.00 gas admissions per day, the 2.90 must be multiplied by 1.73%. The
result shows that there are .05 (2.90 x 1.73%) gassed cases in hospital
on the tenth day in a group of such cases that will die within ten days,
when the daily admission rate from war gases is 1.00 (see Table
27).
The data for the cases who are treated five days or less, six days or
less, etc., are found by the same method.
60. Patients in hospital on any day, when the maximal
one is the tenth, etc. --- The problem here is to find how many cases
there will be in hospital on any one day, such as the fifth or sixth, in
a group of cases whose treatment is for a longer period; for example, ten
days or less. To illustrate the method let us again use the data for
the gassed cases who eventually die. The process is the same as in
Table 31 until the data in the last column are obtained. Then to find the
patients in hospital on any day among those surviving ten days or less,
proceed as shown by Fig. 22. The following
table shows the method in detail.
Table. 33.---Fatal
gassed cases in hospital on any day in a group surviving ten days
or less.
Fig. 77.---Histogram and fitted
skew curve for daily admission rates from diseases and nonbattle injuries
to hospital and quarters per 1000 strength in 30 large camps in the United
States during 1918, excluding September and October.
Fig. 78.---Histogram. and fitted
skew curve for daily admission rates, from diseases and nonbattle injuries
to hospital only per 1000 strength in 30 large camps in the United States
during 1918, excluding September and October.
Fig. 79.---Duration of treatment
(leaving sick report) of diseases and nonbattle Injury cases among white
enlisted men in hospital and quarters in the United States in 1925 -1927.
(1, 2)
Fig. 80.---Duration of treatment
(remaining on sick report) of disease and nonbattle injury cases in hospital
and quarters as they occur in the United States.
NOTE: Observed points from data as graduated by Fig. 79.
(1) By multiplying (2) by 1.8954. (1,2)
(2) From integration of formula for curve.
(3) 15.07 (14.0742 + 1.00) was the average number of days lost per case
in the U. S. in 1918. Multiply (2) by 92.63% to reduce it to (3).
Fig. 81.---Duration of treatment
(leaving hospital) of disease and nonbattle injury cases in hospital as
they occur in the United States.
NOTE: Observed points based upon the same data as is Fig. 79, after
eliminating 91.07 % of them as quarter cases as determined by Sect. I of
Fig. 79. (2)
Fig. 82.---Duration of treatment
(remaining in hospital) of disease and nonbattle injury cases as they occur
in the United States.
NOTE: Observed points from data as graduated by Fig. 81.
(1) From integration of formula for curve.
(2) 20.36 (19.36 + 1.00) was the estimated average number of days lost
per hospital case in the U. S. in 1918 (Fig. 3, p. 7). Multiply (1) by
90.55% to reduce it to (2).
Fig. 83.---Duration of treatment
(leaving hospital) of disease and nonbattle Injury cases which occurred
in the American Expeditionary Forces in 1918 while in the A. E. F. and
later in the U. S.
NOTE: Observed points -from experience with A. E. F. cases during the
last six months of 1918.
Fig. 84.---Duration of treatment
(remaining in hospital) in the American Expeditionary Forces and later
in the U. S. of disease and nonbattle injury cases which occurred in the
A. It. P. In 1918.
NOTE: Observed points from data as graduated by Fig. 83.
Fig. 85.---Duration of treatment
(leaving hospital) in the A. E. F. only of disease and nonbattle injury
cases which occurred there in 1918.
NOTE: Observed points from experience with the A. E. F. cases during
the. last six months of 1918, using only duty cases, deaths, and 40 % of
the cases sent to the U. S. to cover the estimated time lost in the A.
E. F. only. (1)
Fig. 86.--Duration of treatment
(remaining in hospital) in the A. E. F. only of disease and nonbattle injury
cases which occurred there in 1918. (1)
NOTE: Observed points from data as graduated by Fig. 85.
(1) From integration of formula of curve.
(2) It is estimated that the average days lost per case in the A. E. F.
only was 23.75 (22.75 + 1.00).Multiply (1) by 96.575% to reduce it to (2).
Fig. 87.---Duration of treatment
of GAS cases which occurred in the A. E. F. in 1918. (1)
NOTE: The observed points include practically only the time lost by
cases while in the A. E. F. The lower curve (b) is sloped so as to include
only that much time; while the upper one (a) covers all time lost including
that after transfer from the A. E . F. The upper curve is obviously a poor
fit of the observed points, but it is as good a one as is practicable with
the available data.
Fig. 88.---Duration of treatment
of GUNSHOT cases which occurred in the A. E. F. 18.(1)
NOTE: See Note on Fig. 87.
Fig. 89.---Duration of treatment
of disease and non-battle injury cases who were admitted to hospital in
the United States in 1918 and returned to duty..
NOTE: Observed points based upon experience with U. S. cases 1925 1927,
modified to conform to 1918 experience. (1)
Fig. 90.---Duration of treatment
of disease and nonbattle injury cases which returned to duty while in the
A. E. F. in 1918.
NOTE: Observed points based upon experience with duty cases in the A.
E. F. during the last six months of 1918. (1)
Fig. 91.---Duration of treatment
of GAS cases which returned to duty in the A. E. F. in 1918.(#1)
NOTE: Observed points based upon experience with duty cases in the A.
E. F. during the last six months of 1918. (1)
Fig. 92.---Duration of treatment
of GUNSHOT cases which returned to duty in the A. E. F. in 1918.
NOTE: Observed points based upon experience with duty cases in the A.
E. F. during the last six months of 1918. (1)
Fig. 93.---Duration of treatment
of disease and nonbattle injury patients admitted to hospital in the United
States in 1918, who ultimately died.
NOTE: Observed points based upon experience with U. S. cases In 1918
which died. (1)
Fig. 94.---Duration of treatment
of disease and nonbattle, injury patients admitted to hospital in the United
States in 1918, who were ultimately discharged for disability.
NOTE: Observed points based upon experience with U. S. cases in 1918
which were discharged an physically disabled. (1)
Fig. 95.---Duration of treatment
of disease and nonbattle Injury patients admitted to hospital in the United
States in 1918, who ultimately died or were discharged for disability.
NOTE: Observed points based upon experience with U. S., cases who died
(using only one tenth of deaths from influenza and, pneumonia) or were
discharged as physically disabled. (1)
Fig. 96.---Duration of treatment
of disease and nonbattle injury patients admitted to hospital in the A.
E. F. in, 1918, who ultimately died.
NOTE: Observed points based upon experience with A. E. F. disease and
nonbattle injury cases during the last six months of 1918, who died. (1)
Fig. 97.---Duration of treatment
of gas patients admitted to hospital in the A. E. F. in 1918, who ultimately
died.
NOTE: Observed points based upon experience with the patients wounded
by poisonous gases in the A. E. F. in 1918, who died. (1)
Fig. 98.---Duration of treatment
of GUNSHOT patients admitted to hospital In the A. E. F. in 1918 who ultimately
died.
NOTE: Observed points based upon experience with the patients wounded
by gunshot missiles in the A. E. F. in 1918, who died.
Fig. 99.---Relationship of the
number wounded by poisonous gases to those wounded by gunshot missiles.
(3)
NOTE: The same infantry regiment battle days were used as per Fig, 100.
As shown by the graph the number of men wounded by war gases increased
at a slower rate than those wounded by gunshot missiles, actually causing
a gradual decrease in the number of gas cases per one gunshot case as the
latter increases in number. Thus the number wounded by poisonous gases
to each one wounded by gunshot missiles was 1.14 when there were 3 of the
latter, but only .18 to each one when there was 153.
Fig. 100.---Relationship of the
number killed by all causes to those wounded by gunshot missiles or by
poisonous gases in 6,022 battle days for infantry regiments from Jan 1
- Nov. 11, 1918. (8)
NOTE: The infantry regiments used were those of the following Divisions:-
1st, 2nd, 3rd, rth, 26th, 27th, 35th, 42nd, 78th, 79th, and 80th.
The graduated and ungraduated data for those killed in relation to the
number wounded by gunshot missiles were reduced to 68.52% of the total
killed, and to those wounded by poisonous gases to 31.48 %, which was the
same percentage that gunshot and gas wounds were of the total.
The relative number killed decreased 43 % as the number wounded by poisonous
gases increased from 10 to 100 per infantry regiment battle day; while
on the other hand the relative number killed to those wounded by gunshot
missiles remained practically constant as the latter increased from 10
to 100.
.
REFERENCES.*
1. Unpublished statistical tables and records on file
in the office of The Surgeon General, U. S. Army.
2. Annual Report of The Surgeon General, U. S. Army
for each year 1819-1928, inclusive
3. Love, Albert G.: The Medical Department of the United
Army in the World War. Medical and Casualty Statistics, Vol. XV, Part 2.
4. Forry, Samuel: Statistical Report on the Sickness
and Mortality in the Army of the United States, Jan. 1819 to Jan. 1839.
5. Coolidge, Richard H.: Statistical Report on the Sickness
and Mortality in the Army of the United States, Jan. 1839 to Jan. 1855.
6. Coolidge, Richard H.: Statistical Report on the Sickness
and Mortality in the Army of the United States, Jan. 1855 to Jan. 1860.
7. Woodward, Joseph J.: Medical and Surgical History
of the War of the Rebellion, Medical Volume, Part One.
8. Otis, George A.: Medical and Surgical History of
the War of the Rebellion, Surgical Volume, Part One.
9. Annual Reports of the Adjutant General, U. S. Army.
10. Battle Participation of organizations of the A.
E. F. 1917-1918, War Department, 1920.
11. Annual Report of the Secretary of War, 1926.
12. Love, Albert G. and Davenport, Charles B.: Defects
Found in Drafted Men.
13. Report of the First Army, American Expeditionary
Forces; The General Service School Press, Fort Leavenworth, Kas., 1923.
14. Lynch, Charles, etc.: The Medical Department of
the United States Army in the World War. Field Operations, Vol. VIII.
15. Brief History of Divisions, U.S. Army, 1918, Historical
Branch, War Plans Division, General Staff. Mimeographed, 1921.
16. Surgery: The Medical Department of the United States
Army in the World War, Vol. X1, Part I.
*All War Department documents or publications.
 Contents
Contents
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()